The OPUS Way

Mon – Sat 11 AM – 07 PM Kolkata, Bangalore +91 98833 55550

Menu

Foundations: Problem Solving and Data Analysis

About this unit

This unit introduces you to the foundational problem solving and data analysis skills you’ll need on the SAT Math test, starting with more basic examples. Work through the skills one by one or take a unit test to test all of them at once.

Ratios, rates, and proportions: foundations

What are ratios, rates, and proportions?

A ratio is a comparison of two quantities. The ratio of  to b can be expressed as  or a/b.
[Example: Hats and scarves]
A proportion is an equality of two ratios. We write proportions to help us find equivalent ratios and solve for unknown quantities.
[Example: Flour and water]
A rate is the quotient of a ratio where the quantities have different units.
[Example: Flying speed]
 
In this lesson, we’ll:
  1. Learn to convert between part-to-part and part-to-whole ratios
  2. Practice setting up proportions to solve for unknown quantities
  3. Use rates to predict unknown values
You can learn anything. Let’s do this!!
 
Example: There are  students at Du Bois Academy. If the student-to-teacher ratio is 17:2, how many teachers are there?
 

(Ans): We can set up a proportional relationship using equivalent student-to-teacher ratios. If we plug in known values and use x to represent the number of teachers:

         

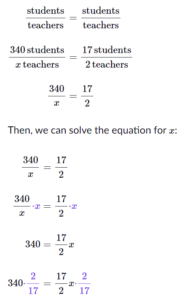
               40 = x.

Unit conversion: foundations

What is unit conversion?

We use units—such as hours, grams, and meters—to measure quantities like time, mass, and distance. But we can use a variety of units to measure the same thing. For example, inches, centimeters, and miles are all measures of distance.
Unit conversion lets us change the units in which a measurement is given.
 
In this lesson, we’ll practice converting between units in a variety of scenarios.
 
Note: You’ll be expected to know the unit equivalencies for time and for metric units of mass, distance, and volume. All other unit equivalencies will be provided for you.
 
You can learn anything. Let’s do this!!
 
Example:  How many inches are in one yard?

Linear relationship word problems: foundations

What are linear relationships?

A linear relationship is any relationship between two variables that creates a line when graphed in the xy-plane. Linear relationships are very common in everyday life.

In this lesson, we’ll:

  1. Review the basics of linear relationships
  2. Practice writing linear equations based on word problems
  3. Identify the important features of linear functions

The skills covered here will be important for the following SAT lessons:

  • Graphs of linear equations and functions
  • Systems of linear equations word problems
  • Linear inequality word problems
  • Graphs of linear systems and inequalities

You can learn anything. Let’s do this!!

Example: A car with a price $17,000 of is to be purchased with an initial payment of $5000 and monthly payments of $240. Which of the following equations can be used to find the number of monthly payments,m required to complete the purchase, assuming there are no taxes or fees?
 

(Ans):  We’re given three important values here: 17000,5000 and 240.

            $17000 is the total price, so that’s what everything else needs to add up to.

            $5000 is a one-time payment.

            $240 is a constant amount that’s paid every month, so it needs to be multiplied by m,the number of months.

           The total price $17000, equals the sum of the other payments: the initial $5000 payment and the $240 paid each month (m).

            17000=5000 + 240m.

Graphs of linear equations and functions: foundations

What are graphs of linear equations and functions questions?

Graphs of linear equations and functions questions deal with linear equations and functions and their graphs in the -plane. For example, the graph of  y = 2x-1 is shown below.
 
An equation in function notation,f(x) = 2x – 1, can also represent this line.
 
In this lesson, we’ll learn to:
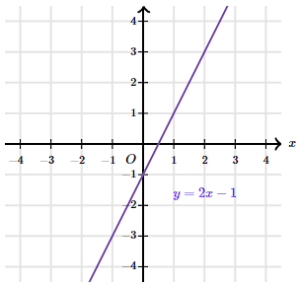
  1. Identify features of linear graphs from their equations
  2. Write linear equations based on graphical features
  3. Determine the equations of parallel and perpendicular lines
You can learn anything. Let’s do this!!
 
Example: What is the slope of the graph of  ?
             
           

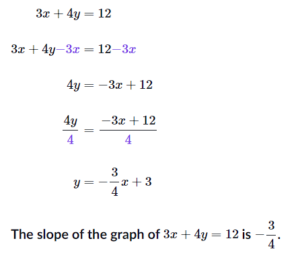
Solving systems of linear equations: foundations

What are systems of linear equations?

A system of linear equations is usually a set of two linear equations with two variables.
  • and 2x – y = 1 are both linear equations with two variables.
  • When considered together, they form a system of linear equations.
A linear equation with two variables has an infinite number of solutions (for example, consider how (0,5),(1,4) , (2,3), etc. are all solutions to the equation x + y =5). However, systems of two linear equations with two variables can have a single solution that satisfies both solutions.
  •  is the only solution to both x + y = 5 and .
In this lesson, we’ll:
  1. Look at two ways to solve systems of linear equations algebraically: substitution and elimination.
  2. Look at systems of linear equations graphically to help us understand when systems of linear equations have one solution, no solutions, or infinitely many solutions.
  3. Explore algebraic methods of identifying the number of solutions that exist for systems with two linear equations.
You can learn anything. Let’s do this!
With OPUS by your side, you're on track for SAT success. Good luck, you've got this!!!!
Shouri Mitra The OPUS Way
Scroll to Top
Call us Now